人工知能とは ②機械学習の手法

機械学習の具体的な手法

教師あり
与えられたデータ（入力）を元に、そのデータがどんなパターン（出力）になるのかを識別、予測する。
■例
・過去の売上から、将来の売上を予測したい。
・与えられた動物の画像が、なんの動物かを識別したい。
・英語の文書を日本語に翻訳したい。
■予測するものが。。。
・数字（連続する値）の場合は回帰問題
・動物画像など（カテゴリー（連続しない値）の場合は分類問題
教師なし
（入力）データそのものが持つ構造・特徴を学習します。
■例
・売上データからどういった顧客層があるのか知りたい。
・入力データの各項目間の関係性を把握したい。
強化学習
＊＊

代表的な手法｜教師あり学習

線形回帰｜Linear Regression

回帰問題
データの分布があった時にそのデータに最も当てはまる直線を考えるというもの。次元が多くても問題はない。
■例
・縦軸が身長、横軸が体重

この線形回帰に正規化項を加えた手法
・ラッソ回帰
・リッジ回帰

ロジスティック回帰｜Logistic Regression

分類問題
任意の値を０〜１の間に写像するシグモイド関数を用いてモデルの出力を行い、基本的にはしきい値を0.5として、出力値が0.5以上であれば正例（+1）、0.5未満であれば負例（0）分類する。しかし、しきい値を、高めや低めに変更することも可能。シグモイド関数のかわりにソフトマックス関数を用いることもある。

ランダムフォレスト｜Random Forest

決定木を利用する手法です。特徴量をランダムに選び出しますので、ランダムな複数の決定木が作られます。データも一部のデータを抽出して利用するブートストラップダンプリングを用います。複数の決定木のそれぞれの結果の多数決を取ることで、高い精度が得れます。
複数のモデルで学習することをアンサンブル学習といい、全体から一部のデータを用い、複数のモデルで学習することをバギングといいます。
ランダムフォレストは、バギングの中で決定木を利用するものとなります。

ブースティング｜boosting

一部のデータを繰り返し抽出して、複数のモデルを学習させるモデル。バンキングとの違いはバンキングは一気に並列にモデル作成しますが、ブーッスティングは逐次モデルを作成するところにあります。逐次作成するので、ランダムフォレストよりも精度が高いが、学習に時間がかかります。
モデルは決定木を利用している。
・AdaBoost
・勾配ブースティング
・XgBoost

サポートベクターマシン｜Support Vector Machine｜SVM

各データ点との距離が最も大きくなるような境界線を求めて、パターン分類を行います。これをマージン最大化といいます。
■課題
・扱うデータは高次元
・データが線形分類できない（直線で分類できない）
データを高次元で写像するアプローチを取るが、それにはカーネル関数を利用する。また、計算が複雑にならないようにすることをカーネルトリックという。

ニューラルネットワーク｜Neural Network

人間の脳の中の構造（ニューロンと神経回路）を模したアルゴリズムです。

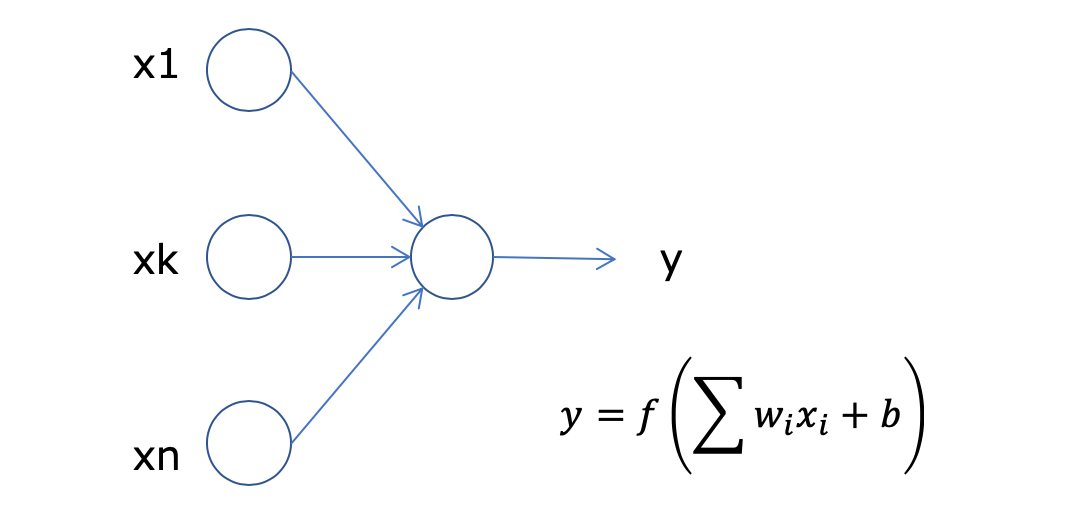
単純パーセプトロン
入力層と出力層、それをつなぐ重みで構成されています。出力を0〜1にする為にシグモイド関数を利用しています。このように層間にどのような電気信号を流すかという調整をする関数を活性化関数といいます。

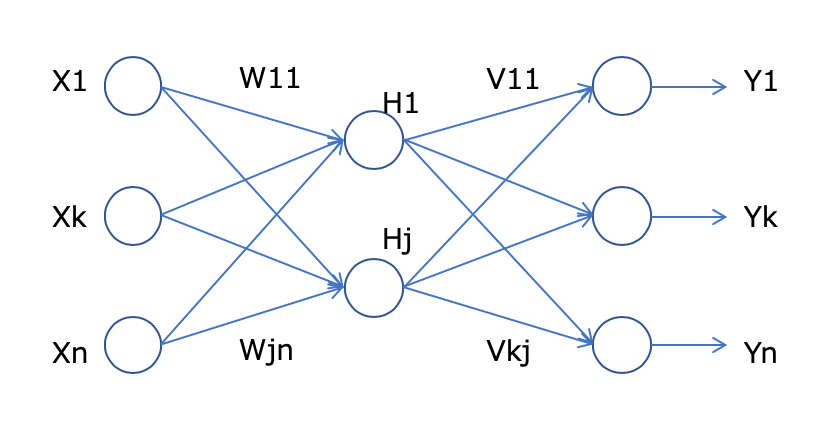
多層パーセプトロン
単純パーセプトロンでは難しい問題は解けないので、更に層を追加するアプローチを取られた構造で多層パーセプトロンといいます。隠れ層（H）が追加され、この隠れ層が幾層にも重ね合わせられていきます。層が増えることで調整すべき重みを増加していきますが、予測値と実際値の誤差をネットワークにフィードバックするアルゴリズムである誤差逆伝播法が考えられたことでも効率的なネットワークにの学習に貢献しました。

代表的な手法｜教師なし学習

k-means

データをｋ個に分けることを目的としている。元データからグループ構造を見つけ出してそれをまとめる。ｋについては人が設定得する。グループをクラスタといい、これを利用した分析をクラスタ分析という。

データをｋ個のクラスタに任意に振り分ける
各クラスタの重心を求める
求まったｋ個の重心と各データの距離を求めて、各データに最も近い重心に紐づけ直す
上記処理を重心がほぼ変化しなくなるまで、繰り返す

この方法で定義されたクラスタの意味を考えるのは人間の仕事になります。

主成分分析｜Principal Component Analysis｜PCA

データの特徴量感の関係性（相関）を分析することでデータの構造を理解する手法である。特徴量が多い場合に用いられる。相関を持つ多数の特徴量から、相関のない少数の特徴量へと次元削減することが目的となる。得られた少量の特徴量を主成分という。

人工知能とは ③ディープラーニング

人工知能とは ①基礎と歴史